Thouless energy

The Thouless energy is a characteristic energy scale of diffusive disordered conductors. It is defined by 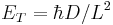E_T = \hbar D /L^2, where D is the diffusion constant and L the size of the system, and thereby inversely proportional to the diffusion time 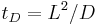t_D = L^2/D through the system.

It was first introduced by the Scottish-American physicist David J. Thouless when studying Anderson localization [1], as a measure of the sensitivity of energy levels to a change in the boundary conditions of the system. Though being a classical quantity, it has been shown to play an important role in the quantum-mechanical treatment of disordered systems. [2]

References

  1. ^ J. T. Edwards and D. J. Thouless, "Numerical studies of localization in disordered systems," J. Phys. C: Solid State Phys. 5, 807 (1972), doi: 10.1088/0022-3719/5/8/007.
  2. ^ A. Altland, Y. Gefen, and G. Montambaux, "What is the Thouless Energy for Ballistic Systems?", Physical Review Letters 76, 1130 (1996), doi:10.1103/PhysRevLett.76.1130.